Στα αεροπορικά ταξίδια, συχνά παρατηρούμε πως οι πορείες των αεροπλάνων δεν ακολουθούν μια ευθεία γραμμή στον χάρτη. Αυτή η ιδιαιτερότητα δεν είναι τυχαία αλλά εξαρτάται από τη γεωμετρία και το σχήμα του πλανήτη μας.
Η γεωμετρία του κόσμου και η έννοια της γεωδαισιακής καμπύλης
Σύμφωνα με τη γεωμετρία που διδασκόμαστε στο σχολείο, γνωστή και ως Ευκλείδεια γεωμετρία, η συντομότερη απόσταση ανάμεσα σε δύο σημεία είναι μια ευθεία γραμμή. Ωστόσο, η Ευκλείδεια γεωμετρία εφαρμόζεται σε επίπεδες επιφάνειες, όπως αυτή ενός χαρτιού, όπου οι διαστάσεις είναι δύο και δεν υπάρχει καμπυλότητα.
Η πιο σύντομη διαδρομή δεν είναι ευθεία; Πώς μας κοροϊδεύουν οι χάρτες!
Η επιφάνεια της Γης, ωστόσο, δεν είναι επίπεδη αλλά κυρτή, γεγονός που οδηγεί στη χρήση μιας διαφορετικής γεωμετρικής προσέγγισης όταν υπολογίζουμε αποστάσεις. Η συντομότερη διαδρομή ανάμεσα σε δύο σημεία πάνω στην επιφάνεια ενός σφαιρικού σώματος, όπως η Γη, είναι μια καμπύλη που ονομάζεται γεωδαισιακή καμπύλη. Στους χάρτες, που παρουσιάζονται σε δύο διαστάσεις, αυτή η καμπύλη εμφανίζεται σαν τόξο, αλλά στην πραγματικότητα είναι η συντομότερη διαδρομή στο τρισδιάστατο σφαιρικό σχήμα του πλανήτη.
Γιατί οι αεροπορικές πτήσεις ακολουθούν καμπύλες πορείες
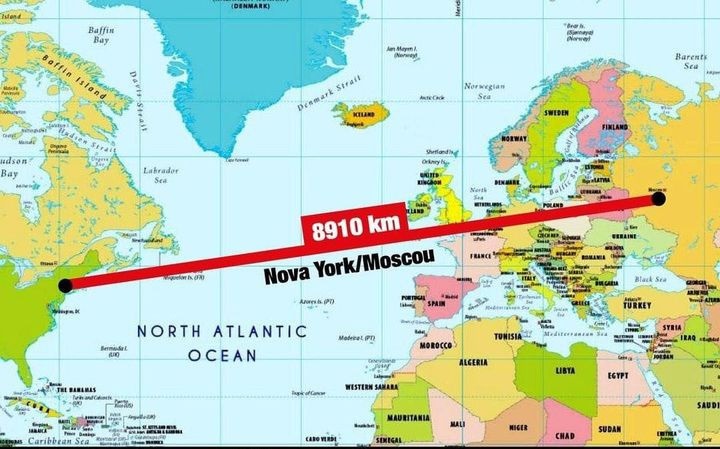
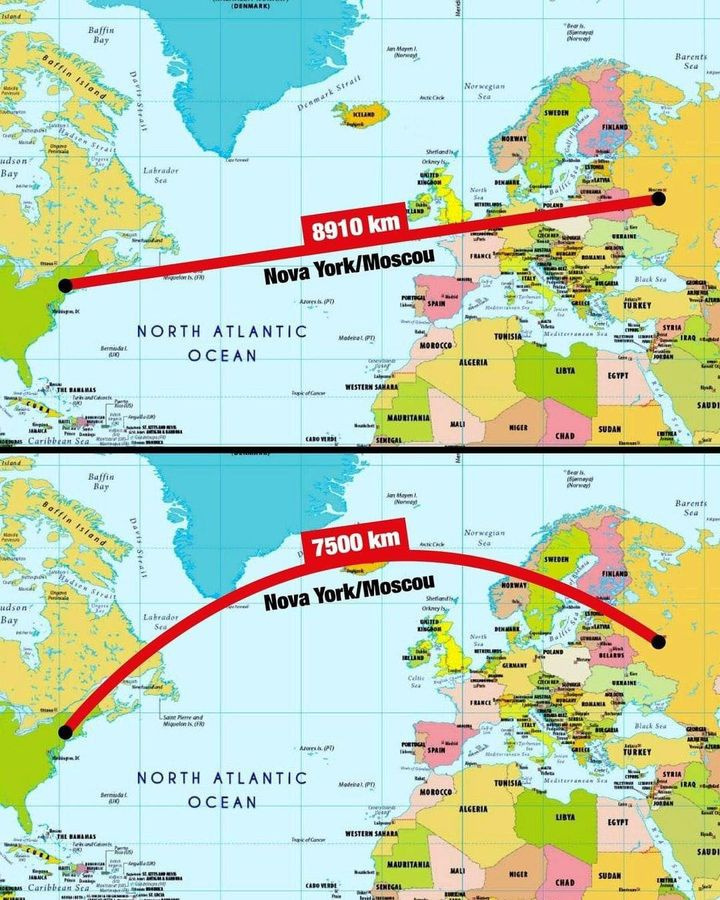
Όταν ένα αεροπλάνο πετά από τη Νέα Υόρκη στη Μόσχα, η διαδρομή που ακολουθεί δεν είναι μια ευθεία στον χάρτη αλλά μια καμπύλη, την οποία βλέπουμε στην παραπάνω εικόνα. Στο πάνω μέρος της εικόνας, η ευθεία γραμμή μεταξύ των δύο πόλεων δείχνει μια απόσταση περίπου 8,910 χιλιομέτρων. Ωστόσο, η πραγματική συντομότερη διαδρομή, που εμφανίζεται ως καμπύλη στον χάρτη, είναι περίπου 7,500 χιλιόμετρα.
Αυτή η διαδρομή φαίνεται καμπύλη στον χάρτη εξαιτίας της αναπαράστασης της σφαιρικής Γης σε επίπεδη επιφάνεια. Στην πραγματικότητα, αυτή η καμπύλη πορεία μειώνει την απόσταση που διανύει το αεροπλάνο και εξοικονομεί καύσιμα και χρόνο, καθιστώντας την πτήση πιο αποδοτική.
Ο ρόλος των προβολών στους χάρτες
Οι χάρτες που χρησιμοποιούμε για να απεικονίσουμε τον κόσμο είναι προβολές, δηλαδή τρόποι να αναπαρασταθεί μια σφαιρική επιφάνεια σε επίπεδο χαρτί. Η πιο συνηθισμένη προβολή είναι η προβολή Mercator, η οποία όμως παραμορφώνει τις αποστάσεις, ειδικά κοντά στους πόλους. Έτσι, όταν κοιτάμε ένα επίπεδο χάρτη, οι γεωδαισιακές καμπύλες, που είναι οι συντομότερες διαδρομές στην πραγματικότητα, φαίνονται σαν τόξα.
Η σημασία της γεωδαισιακής διαδρομής στην αεροπλοΐα
Για να κατανοήσουμε την πρακτική σημασία αυτής της γεωμετρίας στην αεροπλοΐα, αρκεί να σκεφτούμε ότι το κόστος, ο χρόνος πτήσης και η κατανάλωση καυσίμων εξαρτώνται άμεσα από τη συντομότερη και πιο αποδοτική διαδρομή. Χάρη στην τεχνολογία και τους μαθηματικούς υπολογισμούς, τα σύγχρονα αεροσκάφη ακολουθούν αυτές τις γεωδαισιακές διαδρομές, επιτυγχάνοντας πιο γρήγορα και οικονομικά ταξίδια.
Συμπέρασμα
Οι πτήσεις που δεν ακολουθούν ευθείες γραμμές στους χάρτες δεν είναι τυχαίο φαινόμενο, αλλά μια εφαρμογή της γεωμετρίας και της φυσικής στην αεροπορία. Κατανοώντας τις γεωδαισιακές καμπύλες, μπορούμε να εκτιμήσουμε πώς οι αεροπορικές εταιρείες βελτιώνουν τα δρομολόγια, εξοικονομώντας χρόνο και πόρους, ενώ παράλληλα προσαρμόζονται στην πραγματική μορφή του πλανήτη μας.